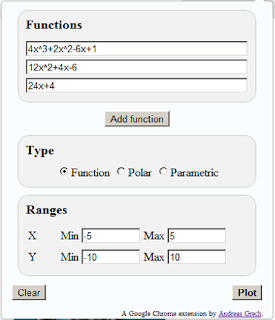
This weekend I got round to writing a Google Chrome extension that aids you in plotting graphs from Wolfram|Alpha. The extension simply takes the parameters you input, constructs a url to Wolfram|alpha and then opens a new tab with that url.
If you wanna give it a go, I published it on the Chrome Web Store.
I've also put the source up at github: https://github.com/dreasgrech/wolframalpha-graphplotter
Wednesday, October 26, 2011
A Chrome extension for plotting graphs with Wolfram|Alpha
Posted by
Andreas Grech
at
6:20 PM

A Chrome extension for plotting graphs with Wolfram|Alpha
2011-10-26T18:20:00+02:00
Andreas Grech
Google Chrome Extensions|Javascript|
Comments
Labels:
Google Chrome Extensions,
Javascript
Sunday, October 9, 2011
Finding a function's inverse with Wolfram|Alpha
To check my answers when calculating the inverse of functions, I've found this handy widget from Wolfram|Alpha which does the job:
Posted by
Andreas Grech
at
1:43 PM

Finding a function's inverse with Wolfram|Alpha
2011-10-09T13:43:00+02:00
Andreas Grech
Mathematics|
Comments
Labels:
Mathematics
Wednesday, October 5, 2011
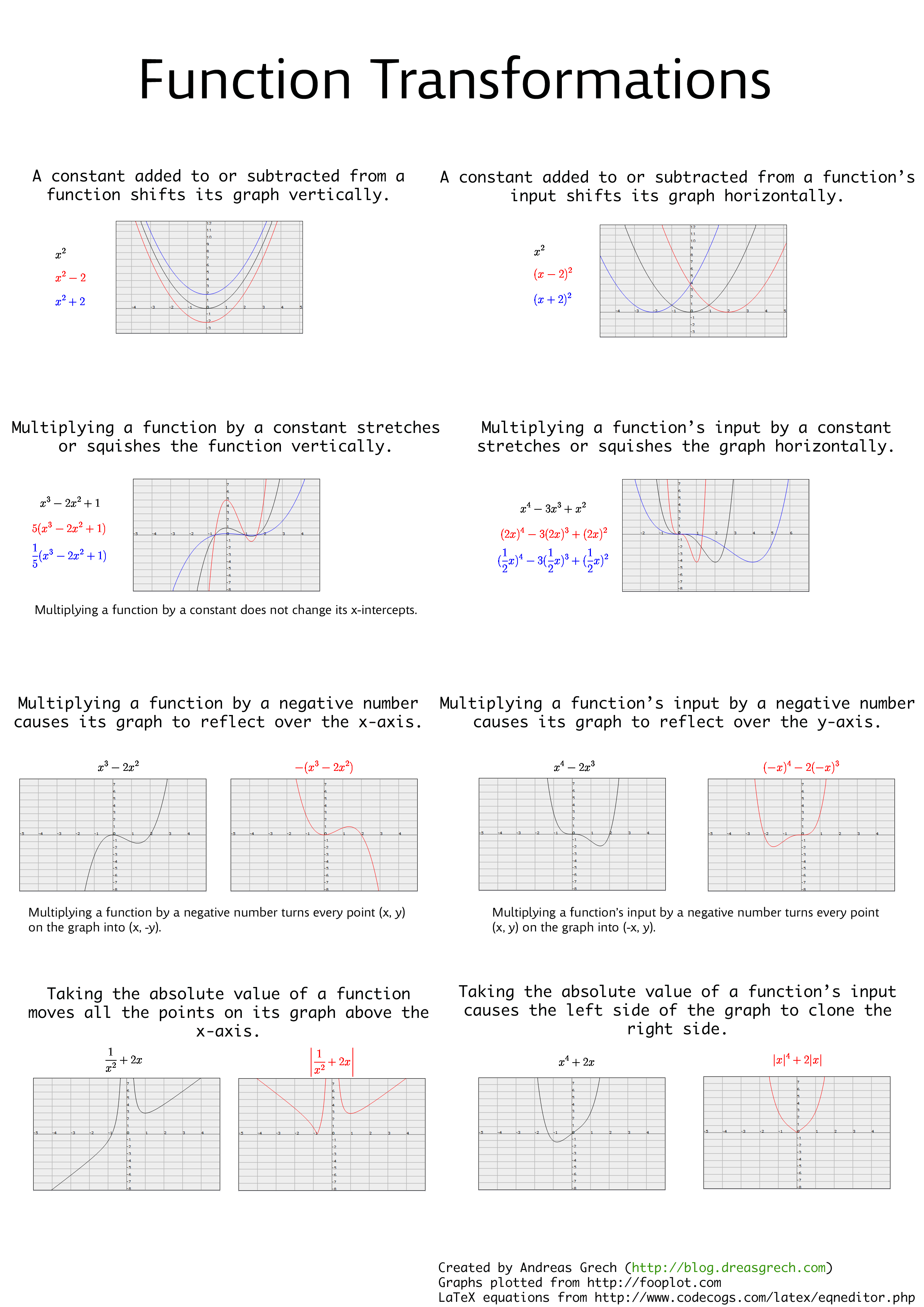
A Function Transformations reference sheet
Since I never miss a change to procrastinate, I decided to spend some time compiling a "cheat sheet" for function transformations.
I've included the following 8 transformations:
I've included the following 8 transformations:
- A constant added to or subtracted from a function shifts its graph vertically.
- A constant added to or subtracted from a function's input shifts its graph horizontally.
- Multiplying a function by a constant stretches or squishes the function vertically.
- Multiplying a function's input by a constant stretches or squishes the function horizontally.
- Multiplying a function by a negative number causes its graph to reflect over the x-axis.
- Multiplying a function's input by a negative number causes its graph to reflect over the y-axis.
- Taking the absolute value of a function moves all the points on its graph above the x-axis.
- Taking the absolute value of a function's input causes the left side of the graph to clone the right side.
Posted by
Andreas Grech
at
7:50 PM

A Function Transformations reference sheet
2011-10-05T19:50:00+02:00
Andreas Grech
Mathematics|
Comments
Labels:
Mathematics
Sunday, October 2, 2011
A State Manager in JavaScript
The following is an implementation for a state manager written in JavaScript. More than one state can be "on" at one moment but mutual exclusivity rules can be set up to allow certain states to not be "on" at the same time i.e. if one of the states is switched on while the other is already on, the latter will be switched off since they can't be both on at the same time.
It also supports two hooks which can be used if you want to be notified when states are changed.
It's implemented with a fluent interface to allow for method-chaining.
The source is here: https://github.com/dreasgrech/statemanager-js
I've set up a simple demo to show how it can be used. You can view it here: http://dreasgrech.com/upload/statemanager-js/demo.html
It also supports two hooks which can be used if you want to be notified when states are changed.
It's implemented with a fluent interface to allow for method-chaining.
The source is here: https://github.com/dreasgrech/statemanager-js
I've set up a simple demo to show how it can be used. You can view it here: http://dreasgrech.com/upload/statemanager-js/demo.html
Basic Usage
var state = stateManager();
state.turnOn("state 1", "state 2");
state.on("state 1"); // true
state.on("state 2"); // true
state.on("state 3"); // false
state.toggle("state 2"); // "state 2" is now off
state.on("state 2"); // false
toggle returns the new state after it's been toggled.Mutual Exclusivity
var state = stateManager();
state.mutex("state 1", "state 3"); // "state 1" and "state 2" now cannot be both on at the same time
state.mutex("state 2", "state 3"); // "state 2" and "state 3" now cannot be both on at the same time
state.turnOn("state 1");
state.turnOn("state 3"); // "state 1" will now be turned off since 1 and 3 are mutually exclusive
state.turnOn("state 1"); // turning "state 1" on, but switching "state 3" off for the same reason
state.turnOn("state 2"); // if "state 3" was on at this point, it would have been switched off
Hooks
var state = stateManager();
state.onStateChanged(function (state, value) { // The global event; fires every time a state changes
console.log(state + " is now " + value);
});
state.onStateChanged("state 1", function (value) { // The event that will only fire when "state 1" changes
console.log("[Custom hook] state 1 has been changed. New value: " + value);
});
state.turnOn("state 1");
state.turnOn("state 3", "state 2");
state.toggle("state 1");
state.turnOn("state 2");
Output:state 1 is now 1 [Custom hook] state 1 has been changed. New value: 1 state 3 is now 1 state 2 is now 1 state 1 is now 0 [Custom hook] state 1 has been changed. New value: 0Note that the onStateChanged event fires only when a state changes. For example, if you turnOn("state 2") while "state 2" is already on, the event will not fire. The same goes for when a state is off and you try to turnOff.
Posted by
Andreas Grech
at
8:48 PM

A State Manager in JavaScript
2011-10-02T20:48:00+02:00
Andreas Grech
Javascript|
Comments
Labels:
Javascript
Saturday, October 1, 2011
Function composition in JavaScript
Function composition is the application of a result of a function as input to another function. Say we have the following three functions:
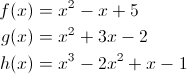
Composing functions f, g and h respectively means that we pass the output from function h as the input to function g and then passing the output from g as the input to function f. Mathematically, it would be represented as follows:
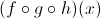
That's essentially the same as:
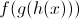
Functions in JavaScript are first class citizens. This means that they can be stored in variables and data structures, passed as an argument to functions and also returned from functions. This means that we can easily implement function composition in JavaScript with a very trivial function:
Here's an example of how we can use it by composing three functions that represent the three polynomials mentioned at the start of the post:
Composing them together would then be:
The result of the composed function is now the same as the result of f(g(h(x))):
If we had a function f and its inverse f-1 and we compose them, we should get the original input x:
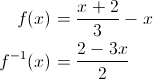
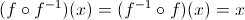
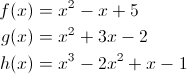
Composing functions f, g and h respectively means that we pass the output from function h as the input to function g and then passing the output from g as the input to function f. Mathematically, it would be represented as follows:
That's essentially the same as:
Functions in JavaScript are first class citizens. This means that they can be stored in variables and data structures, passed as an argument to functions and also returned from functions. This means that we can easily implement function composition in JavaScript with a very trivial function:
Function.prototype.compose || (Function.prototype.compose = function (f) {
var g = this;
return function () {
return g(f.apply(null, arguments));
};
});
Here's an example of how we can use it by composing three functions that represent the three polynomials mentioned at the start of the post:
var f = function (x) {
return x*x - x + 5;
}, g = function (x) {
return x*x + 3*x - 2;
}, h = function (x) {
return x*x*x - 2*(x*x) + x -1;
};
Composing them together would then be:
var composed = f.compose(g).compose(h);
The result of the composed function is now the same as the result of f(g(h(x))):
composed(x) === f(g(h(x))); // true
If we had a function f and its inverse f-1 and we compose them, we should get the original input x:
var f = function (x) {
return (x + 2) / 3 - x;
}, f_inverse = function (x) {
return (2 - 3*x) / 2;
};
(f.compose(f_inverse)(x) || f_inverse.compose(f)(x) || x) === x; // true
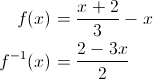
Posted by
Andreas Grech
at
2:17 PM

Function composition in JavaScript
2011-10-01T14:17:00+02:00
Andreas Grech
Javascript|Mathematics|
Comments
Labels:
Javascript,
Mathematics
Subscribe to:
Posts (Atom)