Function composition in JavaScript

Function composition is the application of a result of a function as input to another function. Say we have the following three functions:

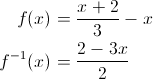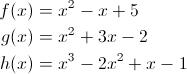
Composing functions f, g and h respectively means that we pass the output from function h as the input to function g and then passing the output from g as the input to function f. Mathematically, it would be represented as follows:

That's essentially the same as:

---

Functions in JavaScript are first class citizens. This means that they can be stored in variables and data structures, passed as an argument to functions and also returned from functions. This means that we can easily implement function composition in JavaScript with a very trivial function:

Function.prototype.compose || (Function.prototype.compose = function (f) {
    var g = this;
    return function () {
        return g(f.apply(null, arguments));
    };
});

Here's an example of how we can use it by composing three functions that represent the three polynomials mentioned at the start of the post:

var f = function (x) {
    return x*x - x + 5;
}, g = function (x) {
    return x*x + 3*x - 2;
}, h = function (x) {
    return x*x*x - 2*(x*x) + x -1;
};

Composing them together would then be:

var composed = f.compose(g).compose(h);

The result of the composed function is now the same as the result of f(g(h(x))):

composed(x) === f(g(h(x))); // true

---

If we had a function f and its inverse f^-1 and we compose them, we should get the original input x:

var f = function (x) {
    return (x + 2) / 3 - x;
}, f_inverse = function (x) {
    return (2 - 3*x) / 2;
};

(f.compose(f_inverse)(x) || f_inverse.compose(f)(x) || x) === x;  // true