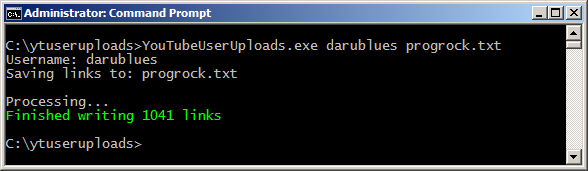
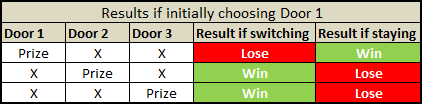
You're on a game show and begin the game by having three doors in front of you. Behind one of the doors, lies the prize. You don't know which door is the winning door but the game show host knows.
You now randomly choose the door which you think has the prize behind it, but the door doesn't open for the time being. In this case, we are going to choose the middle door.
The game show host must now open one of the two remaining doors, and the door he chooses must not be the winning door. For this example, the game show host opens the door on the right.
The host now asks you if you want to stick with your first choice or switch to the remaining door.
Is it to your advantage to change your choice?
To test this out, I wrote some code using JavaScript to simulate playing a number of games and supplying me with the results of how many times it won when switching or not switching the chosen door upon given the choice. The initial guesses are all random.
Results
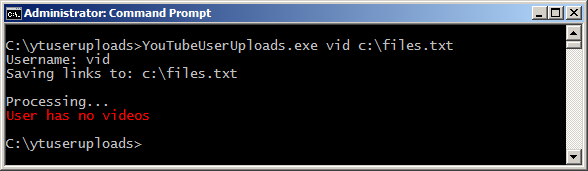
The following is the output for 5 runs with 10,000 games each:
Playing 10000 games
Wins when not switching door 3317
Wins when switching door 6738
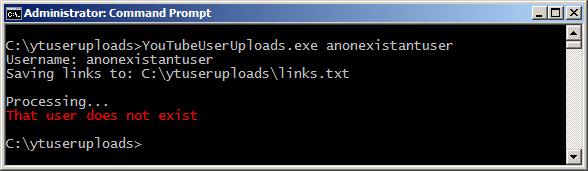
Playing 10000 games
Wins when not switching door 3376
Wins when switching door 6735
Playing 10000 games
Wins when not switching door 3287
Wins when switching door 6726
Playing 10000 games
Wins when not switching door 3298
Wins when switching door 6664
Playing 10000 games
Wins when not switching door 3302
Wins when switching door 6674
These results show how
the number of times you win when switching the door is approximately double the number of times you win when not switching the door.
This may seem counter intuitive at first as you may think that there's a 1/3 chance of winning, but as you can see from the above results, that's actually not the case. In fact, switching the door wins twice as often staying.
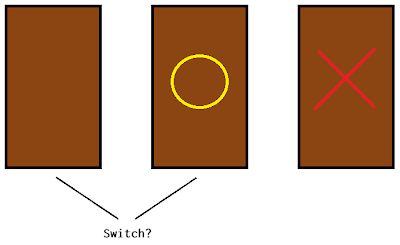
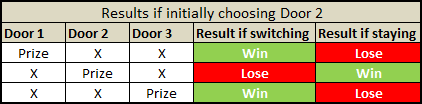
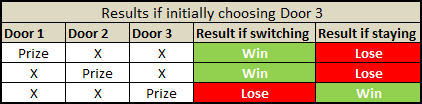
The same goes for when initially choosing Door 2 or Door 3:
Adapted from [Vos Savant, 1990]
Notice how, irrespective of which door you initially choose, you always have 2/3 chance of winning if you then switch.
The code
var totalGames = 10000,
selectDoor = function () {
return Math.floor(Math.random() * 3); // Choose a number from 0, 1 and 2.
},
games = (function () {
var i = 0, games = [];
for (; i < totalGames; ++i) {
games.push(selectDoor()); // Pick a door which will hide the prize.
}
return games;
}()),
play = function (switchDoor) {
var i = 0, j = games.length, winningDoor, randomGuess, totalTimesWon = 0;
for (; i < j; ++i) {
winningDoor = games[i];
randomGuess = selectDoor();
if ((randomGuess === winningDoor && !switchDoor) ||
(randomGuess !== winningDoor && switchDoor))
{
/*
* If I initially guessed the winning door and didn't switch,
* or if I initially guessed a losing door but then switched,
* I've won.
*
* The only time I lose is when I initially guess the winning door
* and then switch.
*/
totalTimesWon++;
}
}
return totalTimesWon;
};
/*
* Start the simulation
*/
console.log("Playing " + totalGames + " games");
console.log("Wins when not switching door", play(false));
console.log("Wins when switching door", play(true));
I've added this piece of code to the Monty Hall problem at the
Rosetta Code website.